Monday, September 23. Today, in Stockholm, members of Working Group I of the UN’s Intergovernmental Panel on Climate Change are meeting to work out, and approve, the group’s contribution to the IPCC’s Fifth Assessment Report. Working Group I (one of three such groups) is the group tasked with reporting on the physical science. Their Summary for Policymakers is scheduled to be released on Friday.
The Fifth Assessment Report (AR5), as the name suggests, is the fifth in a series of reports issued over the years (beginning with the First Assessment Report in 1990), aimed at synthesizing the scientific literature on climate change and its expected impacts. It has been six years since the Fourth Assessment Report (AR4).
I want to talk about something that I, as a philosopher of science, find interesting about these reports, and that is the efforts that the IPCC has made, through the years, to convey judgments about the quality of our knowledge about the climate and the effects of human activity on it. The IPCC has had to pay more attention to these matters than is usual in scientific communication, as the Assessment Reports are not ordinary scientific communications; they are meant to serve as guides for formulating policy on matters of global significance. These decisions (as is often the case) need to be made in the face of less than complete certainty about the consequences of our actions, and this requires a nuanced appreciation of levels of certainty and uncertainty.
One thing that every scientist knows is that there are some areas in which our knowledge is pretty firm, and some in which it is less so (this is, of course, something that scientific knowledge shares with our ordinary everyday knowledge of the world), some things of which we are reasonably certain, others more dubious. One way to represent these gradations of strength of belief is by assigning numbers (perhaps rough estimates) to various propositions, representing how sure you are that they are true. For example, you might be virtually certain that there’s a table in front of you, and we represent this near-certainty via a degree of belief close to one. You might be pretty sure that you’re going to get that promotion, but there are a lot of unknown factors that might get in the way, and we represent this by assigning it a degree of belief considerably less than one.
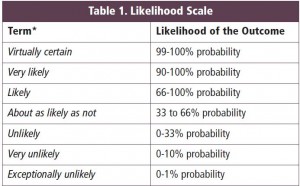
The language we use to express levels of certainty and uncertainty can vary considerably with context and from person to person. To encourage consistency in the use of such language across the various contributions to the Assessment Reports, the IPCC has provide guidelines for authors as to the use of these terms, presented in the following table, from the Guidance Note for Lead Authors of the IPCC Fifth Assessment Report on Consistent Treatment of Uncertainties, taken over unchanged from the Guidance Note prepared for authors of the AR4.
Thus, when you read, in the AR4 Summary for Policy Makers, that “Most of the observed increase in global average temperatures since the mid-20th century is very likely due to the observed increase in anthropogenic GHG concentrations” (p. 5), this is intended to be read as indicating at least 90% certainty.
But how strongly you believe that a statement is true doesn’t exhaust everything there is to say about the quality of your knowledge about that statement. Many years ago, in his book The Logic of Scientific Discovery, the philosopher Karl Popper gave an example that illustrates this.
Consider a coin that you know nothing about; in particular, you don’t know whether it’s a fair coin, or whether it’s biased towards heads, or towards tails. Your degree of belief that the coin will land Heads when tossed might reasonably be equal to your degree of belief that it will land Tails. That is, your degree of belief in each is equal to ½.
Now consider a case in which you have an abundance of statistical evidence about the coin. Let’s say it’s been tossed a million times, and the proportion of Heads and Tails in these tosses is roughly equal. In such a case you have very good evidence that the coin is (at least approximately) a fair coin.
Your knowledge about the coin is different in each case, yet your degree of belief that the next toss will be Heads is the same. Popper found this paradoxical (he called it the “paradox of ideal evidence”), and thought that it could not be adequately dealt with within a subjective approach to probability. Others don’t see anything paradoxical about this, but agree that it points to something important: specifying one’s degree of belief in a proposition (say, about the outcome of the next coin toss) does not suffice to fully characterize one’s state of knowledge about the proposition.
One way to see that there’s a difference is to consider resilience of the judgment in the face of new observations. If you have abundant statistical evidence that a coin is fair, then your degree of belief that the next toss will be Heads will remain close to ½, even if you add to your evidence a series of ten tosses containing eight Heads. Not so if you know nothing about the coin; you would take that series of tosses to be an indication of bias towards Heads.
This is a quality of scientific knowledge that is often obscured by news stories that simply report on the result of the latest study on some matter. What one needs to know, to evaluate the bearing of the study on the matter at hand, is how it fits with other observations and experiments relevant to the topic.
It seems to me that something like this distinction between two dimensions of knowledge, one dimension being degree of belief one might reasonably have, based all the available evidence, and the other an assessment of how well-founded that degree of belief is, is being pointed to in the Guidance Note for Lead Authors of the IPCC Fifth Assessment Report on Consistent Treatment of Uncertainties. In this Note, we find,
The AR5 will rely on two metrics for communicating the degree of certainty in key findings
- Confidence in the validity of a finding, based on the type, amount, quality, and consistency of evidence (e.g., mechanistic understanding, theory, data, models, expert judgment) and the degree of agreement. Confidence is expressed qualitatively.
- Quantified measures of uncertainty in a finding expressed probabilistically (based on statistical analysis of observations or model results, or expert judgment).
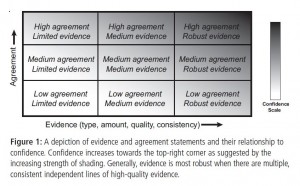
This is accompanied by a chart intended as a guide for assessing the appropriate level of confidence, which is to be based on level of agreement among sources of evidence, and robustness of the evidence.
Robustness is explained as follows: “Generally, evidence is most robust when there are multiple, consistent independent lines of high-quality evidence.”
We thus have two scales on which to evaluate the quality of our knowledge: levels of confidence (expressed quantitatively in the AR4 Guidance Note, and qualitatively in the AR5 Guidance Note), and a likelihood scale (expressed quantitatively, as in Table 1, above).
What does an evaluation of confidence mean? High confidence means that we have robust evidence, with high agreement among the various items of evidence. This need not coincide with being able to attribute a very high likelihood to an event. As the authors of the AR4 Working Group 1 Technical Summary put it, the distinction between confidence and likelihood “allows authors to express high confidence that an event is extremely unlikely (e.g., rolling a dice twice and getting a six both times), as well as high confidence that an event is about as likely as not (e.g., a tossed coin coming up heads).” High confidence in the validity of an assessment of likelihood is not the same as an assessment of high likelihood.
One way to think about Popper’s coin example is to distinguish two kinds of probability. On the one hand we have is the objective probability of Heads, thought to be something out there in the world, and not merely in our heads,. This is 1/2 if the coins is a fair coin, greater than 1/2 if there is a bias towards heads, whether we know it or not. On the other hand there are our degrees of belief about things, which depend on what we know. In particular, we can have degrees of belief in statements about the objective probability.
The quotation I’ve just given from the AR4 WGI TS suggests a similar distinction, between the likelihood of an event, and our degree of confidence that we have accurately assessed the likelihood. If this is what is intended, then it raises the question: what do we mean when we talk of objective, real world probabilities attached to statements about the climate?
Other authors of the AR4 interpreted the confidence/likelihood distinction somewhat differently. There’s a very good discussion of this by two of the authors of the AR5 Guidance Note: Michael D. Mastrandea and Katherine J. Mach in Climatic Change 108 (2011), 659-681. Mastrandea and Mach identify 4 distinct uses of confidence and likelihood terminology in the AR4 report of WGI and WGII.
- Use of either confidence or likelihood terms to characterize different aspects of uncertainties, with confidence assignments characterizing the author team’s judgment about the correctness of a model, analysis, or statement and with likelihood assignments characterizing the probabilistic evaluation of the occurrence of specific outcomes.
- Use of likelihood with inclusion of a confidence evaluation in the likelihood assignment.
- Use of confidence and likelihood terms together in individual statements, sometimes following the interpretation of likelihood and confidence given in approach (1).
- Use of the likelihood or confidence scales “interchangeably,” without clear conceptual distinction.
In the Guidance Note prepared for authors of the AR5, changes are made with the aim of avoiding confusion between confidence and likelihood estimates. For one thing, confidence is not to be expressed in numerical, probabilistic terms, but only in qualitative terms, as “very low,” “low,” medium,” “high,” or “very high.” In most cases, numerical likelihoods are to be assigned only if confidence is high or very high.
Approach (2), which Mastrandea and Mach say is “consistent with a conception of likelihood as the ‘real world’ probability of an outcome occurring… ,” seems to be in line with the two dimensions I have gestured at.
Philosophers of science and formal epistemologists have developed various tools for representing knowledge. Here’s a question: Do we have e tools in hand adequate for handling the dimensions of knowledge I’ve been discussing? If not, what it would take to develop them? It seems to me that this could be of use to scientists in their attempts to communicate the quality of our knowledge, and that there is scope here for frutiful collaboration between philosophers and scientists.
I have some thoughts on how to represent these dimensions of knowledge, which I reserve for a follow-up post. For now, I’d like to hear what thoughts others have on these matters, in the comments.