This blog post celebrates the 50th anniversary of the publication of a particular paper on the foundations of quantum mechanics by physicist and philosopher, John Stewart Bell. “On the Problem of Hidden Variables” was published in the July, 1966 issue of Reviews of Modern Physics. The main objective of this blog is to communicate the contents of the paper to a general audience. However, as a Rotman blogger, I also have the dark and manipulative mission to convince the reader of the value of philosophers engaged with the sciences. It would be nice if the first objective helped with the second, and it does, but I think not obviously so. We’ll get to the propaganda at the end, but, first, the good stuff.
It’s important for the purposes of explaining Bell’s paper to first point out a considerable difference between classical mechanics and the orthodox formulation of quantum mechanics. The classical theory of a particular type of rigid body, like a football, will talk, at least partially, about properties with definite values directly attributable to a particular hypothetical football, and it will state things like the relationships that exist between these properties. For example, it could say that the specific football’s angular momentum is given by the product of its moment of inertia with its total angular velocity. On the other hand, the analogous relationships discussed in orthodox quantum mechanics are between observable operators. Observable operators are bits of mathematics associated with what would classically be unproblematically thought of as intrinsic properties of a system but are just things that we measure in quantum mechanics (whatever that means), like position or momentum. They represent these things in the sense that a given operator encodes the possible values one could get as an outcome by measuring the operator’s corresponding “property” and the probabilities of getting each outcome for each state of the system. So instead of discussing variables with certain definite values directly attributable to a hypothetical individual system, orthodox quantum mechanics ultimately only directly discusses sets of possible measurement outcomes and their probabilities given different states of the system. But surely, you might say, measurements, whatever they are, just reveal some pre-existent, definite value of some property possessed by the system and so the theory does more or less discuss the properties of systems, even if it must make probabilistic claims about the values of these properties (due to some lack of knowledge in this scenario). The picture where the values of specific outcomes are imagined to be values that have obtained all along for the different observables is possible to maintain in a limited sense but it has odd features, one of which comes out in Bell’s 1966 paper and will be discussed below. Remarkably, as non-committal as the operator talk might seem concerning the nature of these hidden variables, imposing the relationships between operators discussed in orthodox quantum mechanics on these variables is sufficient to require embracing one such odd feature when maintaining the otherwise classical picture featuring these variables. Thus, a very general and natural (given our classical heritage) class of pictures of the world is ruled out, and ruled out by relationships that basically just state of the empirical content of quantum mechanics (at least in the sense of content common to every version of quantum mechanics).
The overall objective of Bell’s 1966 paper was to get clear on exactly what the functional relationships between observables postulated by quantum mechanics really meant for the definite values of pre-existent properties directly attributed to individual systems (called hidden variables), if these values are to directly account for measurement outcomes and their statistics. It’s important to first get clear on what the relationship between quantum observables means empirically. One type of relationship derivable from the relationship between observable operators is a relation that holds between expectation values for each observable. The expectation value of an observable is the averaged value of the observable being measured for a given state of the system; it is what would come in agreement or disagreement with an ensemble of repeated measurements of the observable on a series of equivalently prepared systems. The equation relating expectation values of some set of observables for a given state is functionally the same as the equation relating the operators for these same observables (the symbols change while the mathematical operations between them remain the same).
Bell begins his paper clarifying the issue with what had long been taken, by various individuals, as an over statement of the constraint on hidden variables due to the expectation value relationships. von Neumann argued that it is simply impossible to account for these expectation value relationships with individual systems granted properties with values that stand in the same functional relationship. He noted that the properties of a system can only take certain values (you’ve heard about certain stuff in QM only taking particular quantized values) but the equation between them then forces one of the properties to take a value that isn’t allowed. The predicament was taken by von Neumann and followers to mean that a hidden variable theory is impossible, full stop. However, the functional relations considered by von Neumann that could not be satisfied by these definite values were between the expectation values of incompatible observables. You have probably heard about incompatible observables, like position and momentum, in between uninspired sex jokes on “The Big Bang Theory”. What’s relevant is that incompatible observables cannot be measured simultaneously on the same individual system, rather there has to be an ensemble of systems prepared to be in the same state and we do a position measurement on one group of systems to find the expectation value for that measurement on such a system and we do a momentum measurement on a separate group of systems to find the expectation value for this other measurement. So the properties of a given individual system do not actually have to stand in the functional relationship that holds between the expectation values of incompatible observables to account for what measurements on separate systems average to. Thus, it turns out that the relationship does not provide much of a constraint at all on the properties of individual systems, and certainly does not rule out hidden variable theories altogether. Bell also considered another version of the von Neumann argument by Jauch and Piron in the 1966 paper, but he quickly moves on to a stronger argument that avoids the obvious objection above by considering the constraint of relationships between compatible observables.
Compatible observable measurements can be made simultaneously on the same system, and so it is a slightly more reasonable constraint on the hidden variable theory to imagine that the hidden definite values of each property directly attributed to an individual system stand in the same relationship as that which holds between the measurement outcomes for compatible observables. An odd feature of this picture was extracted by Bell from the work of Gleason who was originally just interested in reducing the number of axioms needed to formulate quantum mechanics. A corollary of Gleason’s work was that, for a system of dimension 3 or more (a system that needs the specification of probabilities for 3 or more experimental outcomes of an observable to fully characterize its state), the relationship between expectation values of certain finite sets of compatible observables cannot be satisfied by states committed to definite values of these observable properties. Bell demonstrated the constraint on hidden variable pictures simply and explicitly, however, to unpack what Bell proves, I will actually flesh out the more visually intuitive formulation of an argument to basically the same effect by Kochen and Specker. Bell’s argument at the end of his paper was published before Kochen and Specker’s 1967 paper but Specker alluded to the argument in 1960. Whatever. We call the result: “the Bell-Kochen-Specker Theorem”.
To explain the Bell-Kochen-Specker theorem, it’s important to first explain what constitutes a distinct experimental context to measuring a specific experimental outcome. Two different contexts to finding an outcome could be two different experimental procedures that have the possibility of finding this same outcome (which is the value of some observable). But what’s relevant to distinguishing two procedures that provide two distinct contexts is that the set of possible outcomes differs between the procedures even though they share one common possible outcome. Formally, the distinct contexts imagined in the Bell-Kochen-Specker theorem are represented by observable operators which differ by encoding different sets of measurement outcomes. So while there are trivial senses in which experimental contexts might differ, like in terms of the colour of underwear worn by the experimenter, the relevant sense for the theorem is that the experimental procedures, which could find the same outcome, differ in the other possible outcomes they might find.
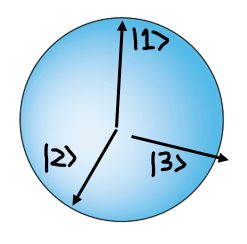
The next step in understanding the theorem is to visualize the different experimental contexts. Think of the three different outcomes, which, along with their probabilities for every given state, uniquely define an observable, as three orthogonal axes with the origin positioned at the center of a sphere.
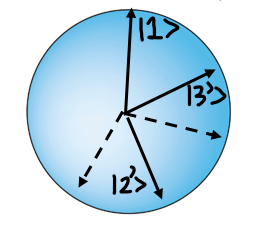
A new distinct observable/context can then be formed by rotating two of the axes about the third.
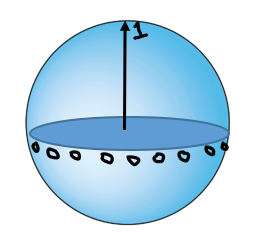
The alternate observables picked out by the new orientations formed by this rotation for any non-zero degree all commute (are compatible) with an observable that is only defined by 2 possible outcomes: whether the outcome represented by the axis of rotation obtains or not. So let’s say that we believed in a picture of reality where this experimental outcome, which is a specific value for some property, obtained all along, independent of its measurement. This means that for every observable of a 3D system that shares the axis representing this obtaining value, the other two orthogonal axes represent values that did not actually obtain all along. So let’s assign a 1 to the point on the sphere intersected by the axis for the value that actually obtains, and let’s assign a 0 to the points on the sphere intersected by the perpendicular axes representing values of observables that therefore don’t obtain for all the different observables that share the axis granted a 1. The assignment of 0’s therefore sweeps out a great circle around the sphere in the plane perpendicular to the axis with the point granted a 1.
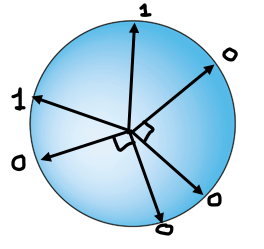
The hidden variable theory under consideration would want to assign a definite value to any given observable property of a system (at least for any arbitrary finite set of observables but it would also seem reasonable to say every observable for a system actually possesses a definite value). The process of assigning definite values to more and more observables can be thought of as the process of assigning one 1 and two 0’s to points on a sphere for more and more sets of 3 orthogonal axes that intersect the sphere at these points.
An intuitive way to see how this process might run into trouble is to consider the fact that the ratio of 0’s to 1’s in this process must always be 2 to 1 but we noted earlier that all points along the great circle perpendicular to the axis with a 1 must be 0’s which demands a much larger ratio of 0’s to 1’s than 2 to 1. It seems reasonable to expect that as we assign more values to more axes we could run into the constraint of too many 1’s or not enough 0’s.
Kochen and Specker found a set of 117 points where assigning two 0’s and a 1 to every orthogonal triple in the set is impossible. Certain points assigned values (1 or 0) in one orthogonal triple are shared with a different orthogonal triple where they must be assigned different values given the constraints on this triple from the others, so the value assignment is not possible. The only way to get out of this predicament is to allow points that belong to more than one orthogonal triple to have different values when considered as belonging to different triples so that we don’t run into a situation where one point is supposed to have conflicting values given the different triples it belongs to. Physically, the required resolution means that certain measurement outcomes must depend on the experimental context which can be understood as a measurement procedure with different sets of other possible outcomes. Even for certain finite sets of observable properties, the outcomes yielded by measurements of these properties could not be the values of the properties possessed by the system all along, independent of the manner in which they were measured. Rather, these values have to be tied to a certain experimental context (the measurement outcome actually depends on exactly how the property was measured). The Kochen-Specker picture makes visually explicit how the relationships that must hold between the different observables do not allow so called “noncontextual hidden variables” for even certain finite sets of observables. Bell took the dependence of any hidden variables on the measurement context to be a vindication of Bohr’s somewhat mysterious view of “the impossibility of any sharp distinction between the behaviour of atomic objects and the interaction with the measuring instruments which serve to define the conditions under which the phenomena appear”.
The situation only gets more constrained for states with dimension higher than three (where observable operators defined on these states are characterized with probabilities for more than three possible experimental outcomes). As an aside, for two dimensional systems, observables would be given by two orthogonal axes and rotating through a third dimension would not produce a distinct context and so would not generate a new context that could conflict with value assignments in the first context which is why the theorem will only apply to states of dimension 3 or more.
Bell’s 1966 paper is an exercise in clarifying what observable talk in quantum mechanics means for a picture of hidden variables recovering certain facts about these observables in a straightforward way. This work is obviously significant but does it really demonstrate the value of philosophers engaged with the sciences (and, a fortiori, the value of the Rotman Institute)? On the face of it, the paper is written by a physicist making mathematical arguments inspired by other mathematicians. Sure, one could note that the motivation for thinking about hidden variable interpretations of quantum mechanics came from discussions mostly relegated to philosophy departments at the time of Bell’s early work, and still today. One could also say that getting clear on what elements of a theory are saying about the world, if correct, is going to involve arguments that are necessarily partially philosophical and that Bell was therefore engaged with philosophy. After all, it’s not like the process of clarifying the implications of observable talk for a certain metaphysical construal of the theory is carried out solely in some formal derivation system, and if we take philosophy to be the enterprise of thinking clearly about what follows from x when the derivation is not a processes of following rules of a formal system, then philosophy would seem to be at play. Additionally, if one wants to add to Bell’s work by moving from constraints on interpreting the theory to claims about the nature of reality, then it’s clear that work like this must already be engaged with views about the possibility and method for gleaning metaphysical insights from scientific theories in general. In summary, one might say that Bell’s work is partially motivated by, infused with, and the stimulus of philosophical thought. However, I think the layperson could grant all this to the example of Bell’s work but still worry about the importance of philosophers engaged with the sciences in the sense that they would be of not much value to the practical aim of theory construction, even though philosophical thought happens to be necessary in forming and articulating the foundations of any discipline including physics and the general framework for theory construction. The concern is that philosophers are not really helping the sciences if philosophical training does not in fact help in the concrete enterprise of coming up with a theory. The fact that the whole enterprise begins and is infused with philosophies typically implicit in the views of physicists does not demonstrate the importance of philosophers and their training to the more concrete task. Let’s consider a position along these lines.
A chapter in Weinberg’s “Dreams of a Final Theory” is called “Against Philosophy” though its target is much narrower. He grants that philosophy does have value outside the sciences and even that the thinking of physicists is guided by certain philosophical views about the nature of their work. However, he is unconvinced that training in philosophy actually helps with anything besides defending against other philosophical views about what a physicist is doing. Even worse, defending certain philosophical positions has provided prejudices against certain avenues to actual theory construction in the past. All his examples of such unhelpful philosophy belong more to general philosophy of science than to the philosophical foundations of a particular physical theory, but, regardless, I can admit that very particular and wrong philosophical positions might be unhelpful while the general enterprise of asking philosophical questions and thinking clearly about them, like philosophers are trained to do, could still be helpful. As for the assertion that philosophical training only helps with defending against other philosophies and not theory construction, it obviously has to be weakened since the necessity of the irrelevance of this training in theory construction would not even be established by plausible looking historical cases for it, even if one could establish only these cases and not counter-examples. (And it seems Weinberg occasionally pulls back from this view). But once the claim is weakened to something defensible, it really just emphasizes the importance of training in things other than philosophy, which should be obvious if the goal is constructing theories in physics. Also, one can still believe this without thinking philosophy is necessarily irrelevant to this process. The appropriate framing of what remains of Weinberg’s issue can be illustrated with Bell’s paper and is basically a way of articulating the mission statement of the Rotman Institute, which is about engaging with the sciences as philosophers. Let’s finish off by making this connection.
Initially, it would seem that Bell’s 1966 paper is not of much help in showing the value of philosophical training in the more concrete task of theory construction, since, on the face of it, the paper is by a physicist who presents simple mathematical arguments inspired by the arguments of other mathematicians, which might in turn have philosophical motivation and significance but that’s irrelevant to Weinberg. Similarly, Kochen and Specker are only mathematicians who asked what a computer scientist would recognize as a colouring problem. However, I think the only thing one should take away from this is the obvious point that if a philosopher wants to do work in the foundations of physics that advances the physics itself, they also need to be trained as mathematical or theoretical physicists to some degree. Bell’s work on issues that were mostly discussed in the philosophical community at the time he was writing exemplifies the importance of his physics training, it does not suggest the unimportance of philosophical training. Familiarity with thinking about colouring problems was obviously important to making the contribution offered by Kochen and Specker but it has no baring on the unimportance of philosophical training in a field that even Weinberg would admit is infused with philosophy. So instead of emphasizing the importance of training in things besides philosophy to do physics, which is all that remains of Weinberg’s point, we can emphasize the importance of this technical training for philosophers if they wish to do physics. Lastly, having non-negligible physics training is a first step in what it ought to mean to be truly engaged with physics as a philosopher. Thus, Bell’s 1966 paper really does illustrate the importance, even in the most specific and pragmatic sense of importance due to Weinberg, of an institute where philosophers engage with the sciences at a non-negligible level, like the Rotman Institute.
Pictured above: Waterfall (M.C. Escher) – Fair use, https://en.wikipedia.org/w/index.php?curid=3473571
Following similar remarks by Penrose about Escher’s Waterfall, Jeffrey Bub draws an analogy between the issue with non-contextual hidden variable theories (discussed at the end of Bell’s paper) and the physical impossibility of Escher’s waterfall in his 2016 book “Bananaworld: Quantum Mechanics for Primates”. The similarity is simply that determinate goings-on at every point in the picture could not actually all obtain and respect the physical relations represented as holding between them. Certain elements like the top of the waterfall belong to two incompatible contexts, one context being that water is coming from the aqueduct and the other being that water is dropping to the aqueduct. Analogously, if definite values for certain observable properties are demanded to be the same in different measurement contexts (ways of measuring them), then not all these values can be assigned and respect the relationships required to hold between them.